
The determinant of a diagonal matrix is if there are non-zero elements in the main diagonal.įigure 1 – Determinant of diagonal matrix A with non-zero entries in main diagonal Rule 2: The determinant of matrix should be non-zero. The remaining two row is not a square matrix therefore, not invertible. The last row of matrix is zero and must be deleted. Rule 1: Diagonal matrix must be a square matrix If the main diagonal has a zero entry then it is a singular matrix for two reasonsĮxample #8 Let matrix be a diagonal matrix of order. The diagonal matrix is a square matrix, but it must have a non-zero entry in the main diagonal to be invertible. Let matrix is raised to power thenĪny matrix is invertible if its determinant is not equal to 0 and it is a square matrix. Įxample #7 Let be a diagonal matrix of order. If a diagonal matrix is multiplied by itself k-times, then we can say that the matrix is raised to the power of. We conclude that the diagonal matrix is symmetric and is true. When we take transpose of a matrix, then becomes, but for a diagonal matrix, therefore, If is a diagonal matrix of order then it is symmetric.Įxample #6 Let be a diagonal matrix of order. Therefore, for diagonal matrices is true. If two matrices and are diagonal matrices of same order, then the multiplication is commutative.Įxample #5 Let be a diagonal matrix of order Numerical Laplace Inversion įixedTalbotNumericalLaplaceInversion.m (3.8 KB) - Mathematica PackageįixedTalbotNumericalLaplaceInversionExample.nb (44.Commutative Property of Multiplication in Between Diagonal Matrices Laplace transform, Numerical inversion, Multiple-precision, Talbot method, Complex arithmetic Mathematics > Calculus and Analysis > Differential Equations P.: Multi-Precision Laplace Transform Inversion, International Journal of Numerical Methods for Engineering, (2003), accepted for publication (IJNME A1032.C) Deatils of the algorith are discussed in the paper Abate, J. The best such method is due to Talbot and this realization gives an improved version of his algorithm. This submission falls into the other group of methods, requiring the evaluation of the transform in the complex plane.
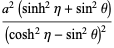
Such an algorithm (GWR) is available from MathSource/4738. One of them uses values of the transform calculated on the real line. There are two main groups of methods for the numerical inversion of the Laplace transform.

In other words, approximate numbers (with decimal point) or Mathematica functions starting with the letter 'N' are not allowed. The Laplace transform should be provided as a function ready for multiple-precision evaluation in the complex plane.

The function calculates the value of the inverse of a Laplace transform at a specified time point. This package provides only one function: FT. Harold Vance Department of Petroleum Engineering Numerical Inversion of Laplace Transform with Multiple Precision Using the Complex Domain Finance, Statistics & Business Analysisįor the newest resources, visit Wolfram Repositories and Archives ».Wolfram Knowledgebase Curated computable knowledge powering Wolfram|Alpha. Wolfram Universal Deployment System Instant deployment across cloud, desktop, mobile, and more. Wolfram Data Framework Semantic framework for real-world data.


 0 kommentar(er)
0 kommentar(er)
